题目:IDA andHankel operatorsonFock spaces
报告人:胡璋剑教授
报告时间:2021年4月23日(星期五),下午15:40 -16:40
报告地点:闻理园A4-216
报告摘要:We introduce a new space IDA of locally integrable functions whose integral distance to holomorphic functions is finite, and use it to characterize boundedness and compactness of Hankel operators on weighted Fock spaces. As an application, for bounded symbols, we show that the Hankel operator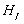 is compact if and only if
is compact if and only if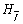 iscompact, which complements the classical compactness result of Berger and Coburn. We also apply our results to the Berezin-Toeplitz quantization and answer a related question of Bauer and Coburn.This is a joint work with Jani A. Virtanen.
iscompact, which complements the classical compactness result of Berger and Coburn. We also apply our results to the Berezin-Toeplitz quantization and answer a related question of Bauer and Coburn.This is a joint work with Jani A. Virtanen.
报告人简介:胡璋剑,湖州师范学院原校长,湖州师范学院二级教授,厦门大学、苏州大学兼职教授、博士生导师;浙江省“151人才工程”第一层次人才、浙江省有突出贡献中青年专家、享受国务院政府特殊津贴专家;在J. Funct. Anal.、J. Geom. Anal.、Math. Z.等期刊发表论文60余篇,成果他引400余次;先后主持国家自然科学基金面上项目4项。科研成果获浙江省科学技术奖一等奖(排名第一)和教育部高等学校科学研究优秀成果自然科学奖二等奖(排名第一)等奖励。
欢迎广大师生参加,联系人:徐庆华教授。